5 結果
FE, RDなどの内生性を想定しないパネルデータの方法と, Arellano-Bondの階差GMMなどの動学パネルデータモデル, OPの方法, そしてCで詳しく紹介するKawaguchiの課題での方法のそれぞれの推定結果を図5.1に示す43. OPの方法は, 多項式回帰とカーネル回帰の両方を試したいところだが, カーネル回帰は既存のパッケージを使いまわせず実装にも時間がかかるので省略した. また, 確率推定をGAMやランダムフォレストに置き換えたケースについても, 結果にほとんど違いがなかったため省略した. Kawaguchiの課題では一般化モーメント法(GMM)で計算しており, その条件の特定は今回のデータとも合致しているが退出行動を省略しているためバイアスが発生することが予想できる(やる気があれば本来の課題との結果の違いを比較すると面白いだろう).
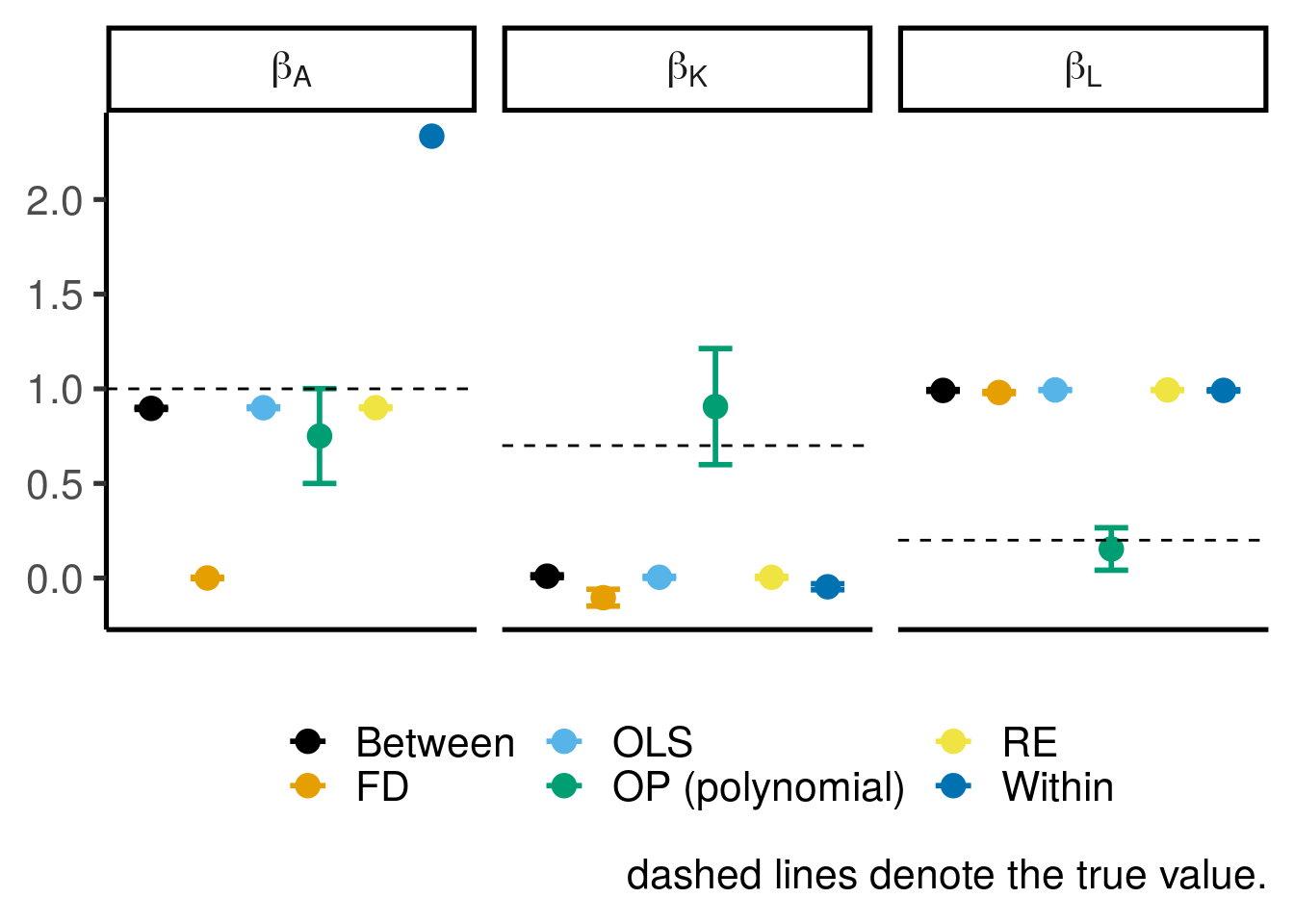
図5.1: 推定結果
それ以外の方法については, 推定された係数のバイアス(真値との差)のみを表5.1に掲載する44
| Model | beta[A] | beta[L] | beta[K] |
|---|---|---|---|
| OP (poly) | -0.250 | -0.046 | 0.206 |
| OP (GAM) | -0.244 | -0.047 | 0.200 |
| OP (RF) | -0.242 | 0.032 | 0.130 |
| OLS | -0.100 | 0.794 | -0.696 |
| Within | 1.335 | 0.791 | -0.746 |
| Between | -0.103 | 0.791 | -0.690 |
| Twoway | 1.331 | 0.792 | -0.741 |
| FD | -0.999 | 0.780 | -0.804 |
| RE | -0.100 | 0.794 | -0.696 |
| AB (twoway) | 1.440 | 0.840 | -0.833 |
| AB (indivi) | 1.550 | 0.818 | -0.987 |
| BB (twoway) | 1.508 | 0.823 | -0.931 |
| BB (indivi) | 6.133 | 1.119 | -6.326 |
| GMM (Kawaguchi) | 0.079 | 0.038 | -0.311 |