A 数値計算上に関係する実装上の注意

非線形最小二乗法は一般に解が一意とは限らない. Olleyらは\(h_{t}:=\hat{\phi}_{t}-\beta_{K}k_{t}\)として計算しており, \(\beta_{A}\)を除いていない. この方法では \(\beta_{A},\omega_{t}\)を識別できないからである(彼らの目的はTFPの計算なので, \(\beta_{K},\beta_{L}\)さえ識別できれば問題にならない). 例えば\(\mathrm{E}\omega_{t}=0\)と分かっているならば識別できるが, 今回の仮定ではそれはわからないため, 数値計算の安定のために\(\beta_{A}\)の減算を省略している.

また, 非線形最適化は初期値を変えると結果が大きく変わることがある. 一般的な解決方法はないが, 今回は生産関数の意味から考えて \(0<\beta_{K}\)という制約を与えている. もし\(\beta_{K}\)がゼロや負なら, 資本投入量を増やしてもまったく生産量が増えないか, むしろ減少することになる. これは通常ならありえないことだろう. optim()関数には lowerというオプションがあるが, ここでは計算速度を損なわないように \(\beta_{K}\)のみ指数変換して計算するように修正している さらに, 初期値を\(1-\hat{\beta}_{L}\)とした. これは, \(\beta_{K}+\beta_{L}=1\)ならば生産関数が規模に対して収穫一定になるからである. もちろんそのようになるという仮定をしていないが, 生産関数のパラメータが極端な値にならないという前提ならば中庸な設定であり, 初期値に向いていると考えられる. この初期値に乱数でばらつきを与えて複数回の結果を確認すると, 初期値と収束した解の対応関係は図A.1のようになり, 次数\(q\)ごとの誤差\(\pm\sigma\)は図A.2のようになった. このように, \(\beta_{K}\)は初期値によって結果にばらつきがあり, \(\beta_{A}\)は初期値に完全に依存していることがわかる. そのため,今回は各次数について100回試行し, 平均値から次数を決定し, その後再びブートストラップ法で反復計算した結果を最終的な推定値として採用することにした.

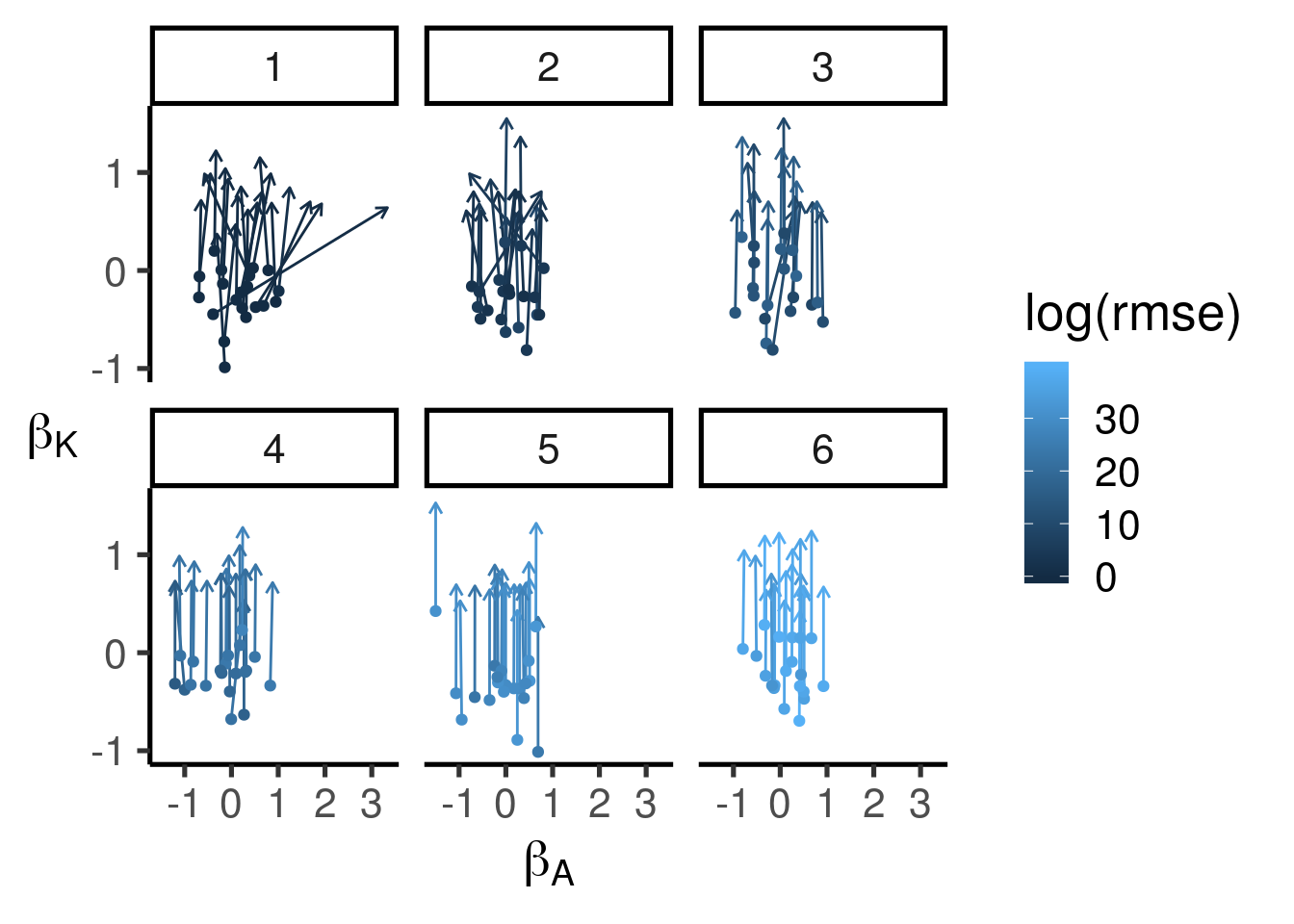
図A.1: 解の初期値と収束先

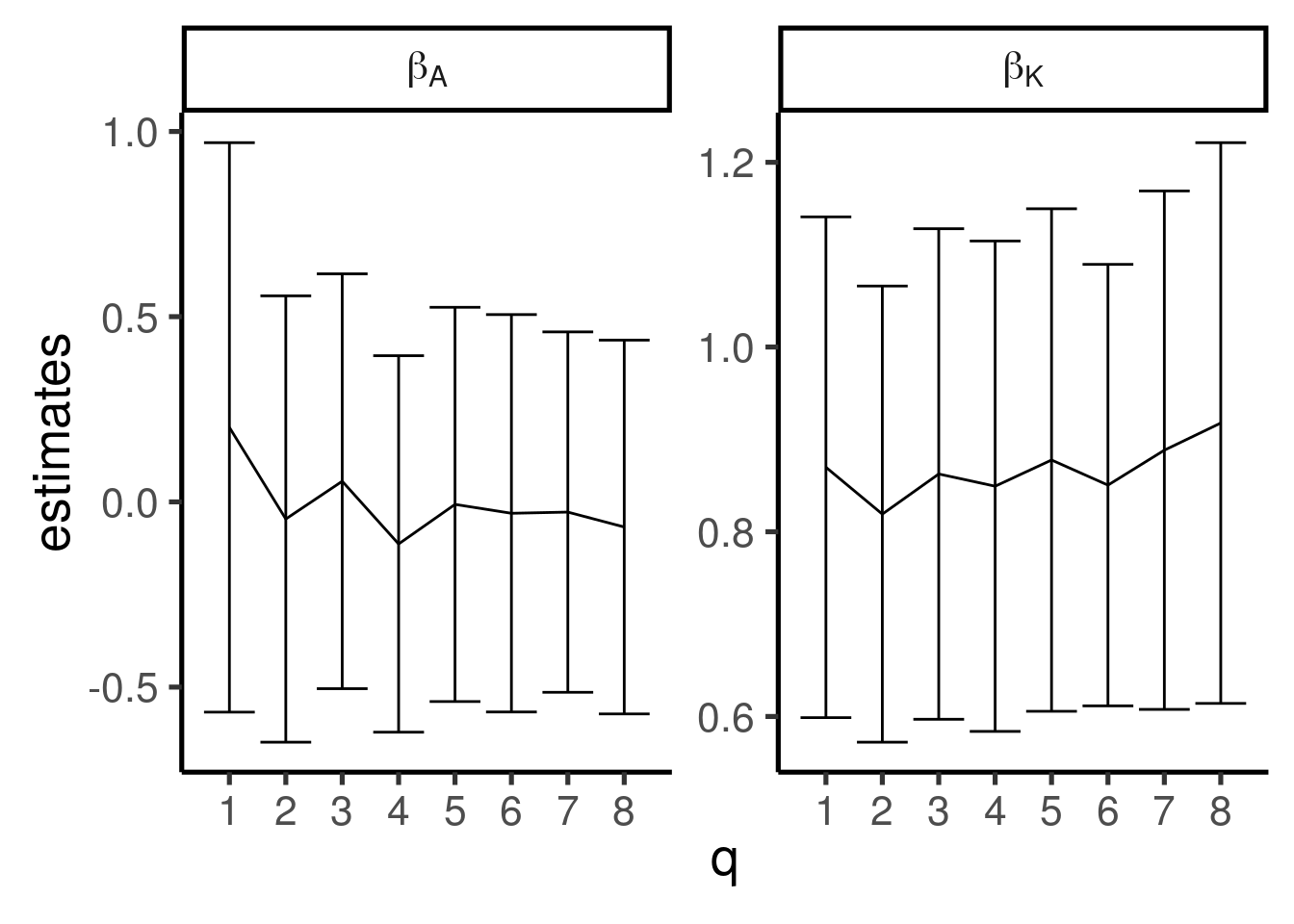
図A.2: 次数ごとの初期値の違いによる誤差

また, 乱数データを生成するパラメータを変更すれば当てはまり易さも変わってくることに注意する. 例えば \(p_{t}\)の推定には\(\mathit{inv},k_{t}\)を使用しているが, もしこれらと\(x_{t}\)との相関が弱ければ, 弱相関操作変数と同様にかえってバリアンスが増加する原因になると予想できるため, 企業のデータを取れば常にOP法をそのまま適用すればいいということはありえないだろう. このような観点からも構造推定は決まったパッケージの決まった構文を実行すれば終わりというものではなく, 各段階で仮説が正しいかを検証する必要がある.