3 どう推定するか
経済学部の計量経済学の講義では, 回帰分析で生産関数の推定をやるところも多いと思う. 前節の生産関数は, \(Y\)を被説明変数, \(K,L\) を説明変数としても線形式ではない. しかし, \(Y,K,L\)がいずれもゼロ以下になりえないことに着目すると, 対数を取って以下のようになる(いわゆる対数線形回帰モデル). \[\begin{gathered}\ln Y=\ln\alpha+\beta_{K}\ln K+\beta_{L}\ln L\end{gathered}\] となる. つまり, おなじみの最小二乗法(OLS)で計算できる. 観測できなかった\(\alpha\)も, 切片パラメータ として推定できることになる. 以降はそれぞれの対数を\(y,\beta_{A},k,l\)に置き換えて, \[\begin{aligned} y &= \beta_{A}+\beta_{K}k+\beta_{L}l+\varepsilon\end{aligned}\tag{3.1}\] という線形回帰モデルを考える. しかし以前書いたように, 経済学の文脈では非線形だろうが線形式だろうがデータに関数を当てはめただけでは用をなさない. 経済理論に即して, 発生しうる問題を排除した方法で推定しなければならない. つまり, 現在ではOLSでは生産関数のパラメータを推定するには不十分と考えられている.
発表時間の問題から, スライドでは大幅に省略しているが, ここでは冗長気味にパネルデータ分析の発展の経緯も合わせて説明していく11.
現在の経済学の観点からすると, (3.1)をそのままOLSで推定するのをためらう大きな理由は以下の3つである.
企業特有の効果が存在する
需要要因を考慮していない
セレクションバイアス
3.1 なぜ生産関数を知りたいのか
しかし, テクニカルなことを説明する前に, そもそもなぜこのようなことをするのかを表明したほうがよかろう. 今回, 最後に紹介するのは Olley and Pakes (1996) の研究で, 彼らは法規制が産業の生産性にどう影響するかを知ることを研究目的としていた. では, 生産性なるものをどう計測すればいいのだろうか.
経済学には全要素生産性 (TFP; total factor productivity)という概念がある. これは, 投入したリソースの量では説明できない生産量の多さを生産性と定義した概念で, 実際には推定した生産関数による生産量の予測値 (理論値) と実測値の誤差で計測する . 例えば今回はコブ=ダグラス型関数で, モデルの仮定から, 物的・人的リソースによる生産量は\(K^{\beta_{K}}L^{\beta_{L}}\)の部分になる. よってTFPを計算する式は, \[\begin{aligned}\mathit{TFP}:= & \frac{Y}{K^{\beta_{K}}L^{\beta_{L}}}\end{aligned}\] となる. もしTFPを毎年計測して値に変化があるのなら, それは技術進歩に由来する生産性の向上であると見なせる(正確にはこれはソロー残差とか成長会計モデルとか呼ばれる)12.
さらに, (3.1)からも分かるように, 対数の性質には \(\ln(x/y)=\ln x-\ln y\)というものがある(高校数学でも扱うはずだ). よって, 仮に(3.1)の係数パラメータ\(\beta_{K},\beta_{L}\)を求められれば, \[\begin{aligned} \ln(\mathit{TFP}):= & y-\hat{\beta}_{K}k-\hat{\beta}_{L}l\\ \therefore\mathit{TFP}= & \exp(y-\hat{\beta}_{K}k-\hat{\beta}_{L}l)\end{aligned}\] となる. よって回帰分析で推定した式を使うと, TFPは\(\alpha\)だけでなく誤差項も含まれることになる. TFPは回帰モデルの残差に依存する.
ではここで, 当てはまりの良さのために生産関数の形状を変えたらどうなるだろうか? 当てはまりを良くするのなら, いろいろなモデルを試していくらでも生産量の予測誤差の少ないモデルを作り出すことができる. しかしそこから計算した残差は一体何を意味するのだろうか? 機械学習や統計モデリングというと, MSEとか対数損失がどれくらい小さいかというのがモデルの良さの指標だと語られることがしばしばあるが, しかしこのようにそれが活用方法としての全てではない.
そしてTFPや生産性といった概念は, このように生産構造をどう仮定するかに強く依存することに注意する. 分析にはかならず「ある仮定のもとで…」という前置きが存在する. 「生産性」という抽象的な概念が何を意味するのか, 何を言っているのかはよく考えるべきであろう13.
3.2 パネルデータ分析と観測されない効果
「企業特有の効果」とは, 特定の企業だけが「特殊な技術を持っている」「優秀な人材が集まっている」など, 単純な量だけでは捉えきれない情報を意味する. つまり, 企業ごとに異なる\(\omega_{i}\)が生産量に影響していると考える. \[\begin{aligned} y_{i}= & \beta_{A}+\beta_{K}k_{i}+\beta_{L}l_{i}+\omega_{i}+\varepsilon_{i}\end{aligned}\] \(\omega_{i}\)は観測できないので, このまま \((y_{i},k_{i},l_{i})\)のデータで回帰すると, \(\omega_{i}\)は定数項\(\beta_{0}\)または誤差項\(\varepsilon\)に吸収される. \(\omega_{i}\)が\(k_{i},l_{i}\)と全く相関しない変数ならば, \(\beta_{A}\)と\(\omega_{i}\)を識別できないものの, 少なくとも\(\beta_{K},\beta_{L}\)の推定はできる.
このような問題をどう解決すれば良いだろうか? まずは問題1だけを考えよう. \(\omega_{i}\)は観測できないが, では推定できないだろうか? つまり, 同一の企業の情報を何度も観測しすれば, そこから推定できないか, というアイディアである. これがパネルデータ分析のスタート地点になる. パネルデータとは, 同一個体を追跡して複数時点で観測したデータである(表3.1).
| 企業ID | 時期 | 生産量 | 資本 | 労働力 |
|---|---|---|---|---|
| 001 | 2019Q1 | 100 | 10 | 10 |
| 001 | 2019Q2 | 110 | 11 | 10 |
| 001 | 2019Q3 | 90 | 12 | 12 |
| 001 | 2019Q4 | 120 | 14 | 13 |
| 002 | 2019Q1 | 80 | 5 | 5 |
| 002 | 2019Q2 | 90 | 6 | 5 |
よって, 企業\(i=1,\cdots,N\)ごとに, \(t=1,\cdots,T\)の観測がある. そこで以降は回帰モデルを以下のように書く.
\[\begin{aligned} y_{i,t}= & \beta_{A}+\beta_{K}k_{i,t}+\beta_{L}l_{i,t}+\omega_{i}+\varepsilon_{i,t}\end{aligned}\tag{3.2}\]
ここではひとまず, \(\omega_{i}\)が企業\(i\)ごとに異なるが, 時間\(t\)に対しては変化しないと考えておこう. また, 問題1だけを考えるにあたって, \(\omega_{i}\)は\(k_{i,t},l_{i,t}\)と相関しないとしておこう. このような\(\omega_{i}\)を観測されない個別効果(unobserved indivisual effect) という.
さらに追加の仮定として, \(\omega_{i}\)が定数である場合, ダミー変数を作成することでOLSであるかのように\(\omega_{i}\)を推定できる14. これをLSDV推定量という. また別の解き方としては, (3.2)を企業ごとに平均を取った場合を考える. \[\begin{aligned} \bar{y}_{i}= & \beta_{A}+\beta_{K}\bar{k}_{i}+\beta_{L}\bar{l}_{i}+\bar{\omega}_{i}+\varepsilon_{i,t}\end{aligned}\tag{3.3}\]
このとき, \(\omega_{i}\)は企業ごとに一定なので, \(\bar{\omega}_{i}=\omega_{i}\)である. よって, (3.2)から(3.3)を引いてからOLSで計算することでも同じ推定結果が得られる. こちらの方法は固定効果(FE; fixed effect)推定量またはグループ内(within)推定量と呼ばれる15.
一方で, \(\omega_{i}\)が定数項ではなく確率変数の可能性もある. つまり, 企業ごとに異なる\(\omega_{i}\)は実は期待値をとればゼロになる確率変数にすぎず, 定数項に見えたものは確率的なゆらぎに過ぎないかもしれない. この仮定の元に考案されたのが変量効果(RE; random effect)モデルである. REモデルは数学的に分散不均一な回帰モデルと同一のため, 実質的に一般化最小二乗法(GLS)と同じである16..
3.3 動学パネルデータ分析
このように, 観察できない要因があってもパネルデータがあれば理論上は推定が可能になる. しかし, Mairesse (1990)17はこれまで紹介した方法とほぼ同じやり方で企業の生産関数を推定したところ, 観測されない効果を識別しようと複雑に差分を取れば取るほど, 係数の推定値が小さくなることを発見した. 彼はこの原因の仮説をいくつか挙げている.
内生性の問題. 個別効果\(\omega_{i}\)は物理的なものではなく, 環境, 経営者の手腕といったものに由来するのなら, 他の説明変数\(k,l\)の決定に影響している.
企業の意思決定のラグ. 経営者が誤差項として現れる短期的な変化, つまり直前の\(\varepsilon_{i,t-1}\)に対応して\(k_{i,t},l_{i,t}\)を決定しているなら, 誤差項と説明変数が相関しており, 単純な差分では推定できない.
同時決定の問題.
測定誤差. 各変数に測定誤差があれば, 差を取ることで打ち消される.
これらの問題への対応として考えられるのが, 操作変数である. (3.2)に, 被説明変数\(y_{i,t}\)の自己回帰項を追加する.
\[\begin{aligned} y_{i,t}= & \beta_{A}+\beta_{K}k_{i,t}+\beta_{L}l_{i,t}+\rho y_{i,t-1}+\varepsilon_{i,t}\end{aligned}\tag{3.4}\]
こういう自己回帰項を含むモデルを扱う分野はパネルデータ分析のなかでも特に動学パネルデータ分析と呼ばれる. このあたりの問題も 奥井 (2016) や Wooldridge (2010), Ch. 11 で丁寧に説明されている18ので冗長だが, 一応簡単に述べておく.
前節のアイディアを流用すれば, Within推定量の応用で時間平均\(\bar{y}_{i}=(T-1)^{-1}\sum_{t=2}^{T}y_{i,t}\)を取ることが考えられる. しかし, パネルデータでは\(N\)が大きいが\(T\)は小さいことが多いため, 一致推定量とみなせない. 一方で, 1階差分(FD) 推定量というものがある. これはある意味DID推定量と同じである. 差分演算子を \(\Delta x_{t}:=x_{t}-x_{t-1}\)というふうに定義する. (3.4)の両辺から\(y_{i,t-1}\)を引くと, 以下のようになる. \[\begin{aligned} \Delta y_{i,t}= & \beta_{K}\Delta k_{i,t}+\beta_{L}\Delta l_{i,t}+\rho\Delta y_{i,t-1}+\Delta\varepsilon_{i,t}\end{aligned}\] しかし, \(\Delta y_{i,t-1}=y_{i,t}-y_{i,t-1}\)から, \(\Delta\varepsilon_{i,t}=\varepsilon_{i,t}-\varepsilon_{t-1}\)と相関が存在する. そこで, \(\varepsilon_{i,t-1}\)より過去の\(y_{i,t-2},\cdots\)を操作変数として使う方法が提案されている. それが Anderson and Hsiao (1981);Anderson and Hsiao (1982) モデルや, Arellano and Bond (1991), Blundell and Bond (1998) のGMM推定法である(いわゆる階差GMMとシステムGMM). しかし, これらは実際に操作変数として意味のある変数なのかということを深く議論せずに\(\{y_{i,t-2},\cdots\}\)を操作変数に利用している. その場合, 上記で挙げたような意思決定が存在するかどうかを検証できないし, これらの推定量には過剰識別や弱相関操作変数の問題が発生することが指摘されており, 妥当性に疑問が残る.
3.4 企業内部の意思決定を考える
しかし, 経済学の理論では, 観察される経済データは市場が需要と供給のバランスを取った結果である. これが2つ目の「需要要因を考慮していない」という話になる. 企業が需要を全く考えずに事業計画を立てるとは考えにくいため, この\(\omega_{i}\)が間接的に\(k_{i},l_{i}\)に影響している可能性は十分ある. また, 企業は新規立ち上げだったり倒産したりする. 現実のパネルデータはしばしば欠落がある. そのようなデータでそのまま推定しようとしたらどうだろうか.
このようなパネルデータでの内生性に対処する推定方法に関する研究はいくつもあり, 特によく出てくるものとしてFEIVモデル, がある.
さらに, Olley and Pakes (1996), Levinsohn and Petrin (2003) はこれらの動学パネルデータ分析の方法から一歩進んで, 企業の意思決定の構造をモデル化した生産関数を考え19, 操作変数を使わずに内生性の問題に対処した方法を提案している (一般にはOPの方法はコントロール関数アプローチと呼ばれる)20.
そこで今回はOlleyらのフレームワークを詳しく説明する. なお, 以降は(3.2)式をもとに説明するが, 各企業で同じことが言えるため\(i\)を省略して書く. OPでは, 観察されない効果\(\omega_{t}\)は企業の経営者は知ることができるが, データとして現れないため分析者には観測できない, 企業固有の生産能力を表す成分である. \(\omega_{t}\)は他の変数の影響を受けない(外生的)が, 自身の過去の値からは影響を受けると仮定する. つまり1次のマルコフ過程であるとする. \[\begin{aligned} \omega_{t}\sim & P(\omega\mid\omega_{t-1})\end{aligned}\]
\(t\)期の始めに経営者は\(\omega_{t}\)を観測して, これをもとに今期の経営計画を決定, つまり, 純キャッシュフローの割引現在価値を最大化できるように\(k_{t},l_{t}\)を決めていると仮定する. そこで, 動学的なモデルを想定する. 企業の\(t\)時点現在での収益を\(\pi_{t}(\omega_{t},k_{t},l_{t})\)として, 投資\(\mathit{inv}_{t}\)に対する費用を \(c(\mathit{inv}_{t})\)とする. 経営者が最適化する現在の価値関数 (value function)を \(V_{t}(\omega_{t},k_{t},l_{t})\)とすると21, 動学モデルでは単に現在の価値関数を最大化することが最適化に繋がるとは限らない. 経営者は, これらを把握した上で, 割引現在価値を最大化するように行動する. つまり, 以下のような \(V^{\ast}\)の達成を目指す. \[\begin{aligned} V^{\ast}= & \max_{\{k_{t},l_{t}\}}\sum_{t=0}^{\infty}\delta V_{t}(\cdots)\end{aligned}\]
これは無限和なのでそのまま計算するのは難しいが, 一定の条件下では上記の最適化問題の解が以下(3.5)のようなベルマン方程式 (Bellman equation) の解と同じであることが分かっている22.
\[\begin{aligned} V_{t}(\omega_{t},k_{t},l_{t})= & \max_{k_{t},l_{t}}\left\{ \Phi,\sup_{i_{t}\geq0}\pi_{t}(\omega_{t},k_{t},l_{t})-c(\mathit{inv}_{t})+\delta\mathrm{E}\left[V_{t+1}(\cdots)\right]\right\} \end{aligned}\tag{3.5}\]
ベルマン方程式が意味するところは, \(t,t+1\)という2時点間の関係さえ分かれば上記の無限和の問題も解けるということである.
ただし, このモデルでは2つの仮定を追加していることに注意する. 1つは, (3.5)には, \(\Phi\)という選択肢があることだ. これは退出, つまり工場の閉鎖や事業を売却することで得られるキャッシュフローである. よって, このモデルでは採算が合わないと判断した経営者が事業撤退を選択する可能性も考慮している. もう1つは, 動学的な決定の必要があるのは\(k_{t}\)のみで, \(l_{t}\)は毎期独立して決定されるように仮定している点である..
では, \(k_{t}\)の動学的な意思決定がどのようになされるかを考えていく. 資本\(k_{t}\)は, 前期のストック\(k_{t-1}\)と, 減価償却率 \(\delta\), そして新規の投資額 \(\mathit{inv}_{t-1}\)の和で表現できる.
\[\begin{aligned} k_{t}= & \mathit{inv}_{t-1}+(1-\delta)k_{t-1}\end{aligned}\]
企業の退出ルールと投資関数を以下のように定義できる. \(t\)期に企業が存続するなら\(x_{t}=1\), そうでないなら\(0\)として, \(x_{t}\)は以下のように決定される. \[\begin{aligned} x_{t}= & \begin{cases} 1 & \text{if }\omega_{t}\geq\underline{\omega}_{t}(k_{t})\\ 0 & \text{otherwise} \end{cases}\end{aligned}\] \[\begin{aligned} \mathit{inv}_{t}= & \mathit{inv}_{t}(\omega_{t},k_{t})\end{aligned}\tag{3.6}\] ここから, 企業が\(t\)期も退出せず操業を続ける確率は \[\begin{aligned} p_{t}:= & \mathrm{P}(x_{t}=1\mid\underline{\omega}_{t}(k_{t}))\\ = & \mathrm{P}(x_{t}=1\mid k_{t},\omega_{t},\underline{\omega}_{t})\end{aligned}\tag{3.7}\] のように\(k_{t},\omega_{t},\underline{\omega}_{t+1}\)の条件に依存することを覚えておこう23. 退出による利益\(\Phi\)は観測できず, 別の変数で表現する必要があるため, 退出を決定するしきい値を表す関数\(\underline{\omega}_{t}(\cdot)\)を導入する.
利潤関数\(\pi_{t}\)が\(k_{t}\)に対して減少関数なら, 価値関数にとっては増加関数, そして資本ストックの多い企業は一時的な生産性の変化\(\omega_{t}\)とはあまり関係なく, 将来に比較的大きな収益が見込まれるから, しきい値\(\underline{\omega}_t(\cdot)\)は比較的低くなるはずなので\(\underline{\omega}_{t}(\cdot)\)は減少関数になる(退出確率\(p_{t}\)の減少)はずだ. よってこの退出ルールから\(\omega_{t+1}\)に\(x_{t+1},k_{t+1},l_{t+1},\omega_{t}\)を条件付けた\(\omega_{t+1}\)の期待値 \[\mathrm{E}\left[\omega_{t+1}\mid k_{t+1},\omega_{t},x_{t+1}=1\right]\] は\(k_{t+1}\)に対して減少関数であるとわかる (\(l_{t+1}\)は独立しているので\(\omega_{t+1}\)に影響しない). これが観測できない生産性 \(\omega_{t}\)と資本\(k_{t}\)が相関していることの理由付けになる.
ここまでで登場した変数間の関係をグラフィカルモデルで描くならば, 図3.1のようになる.
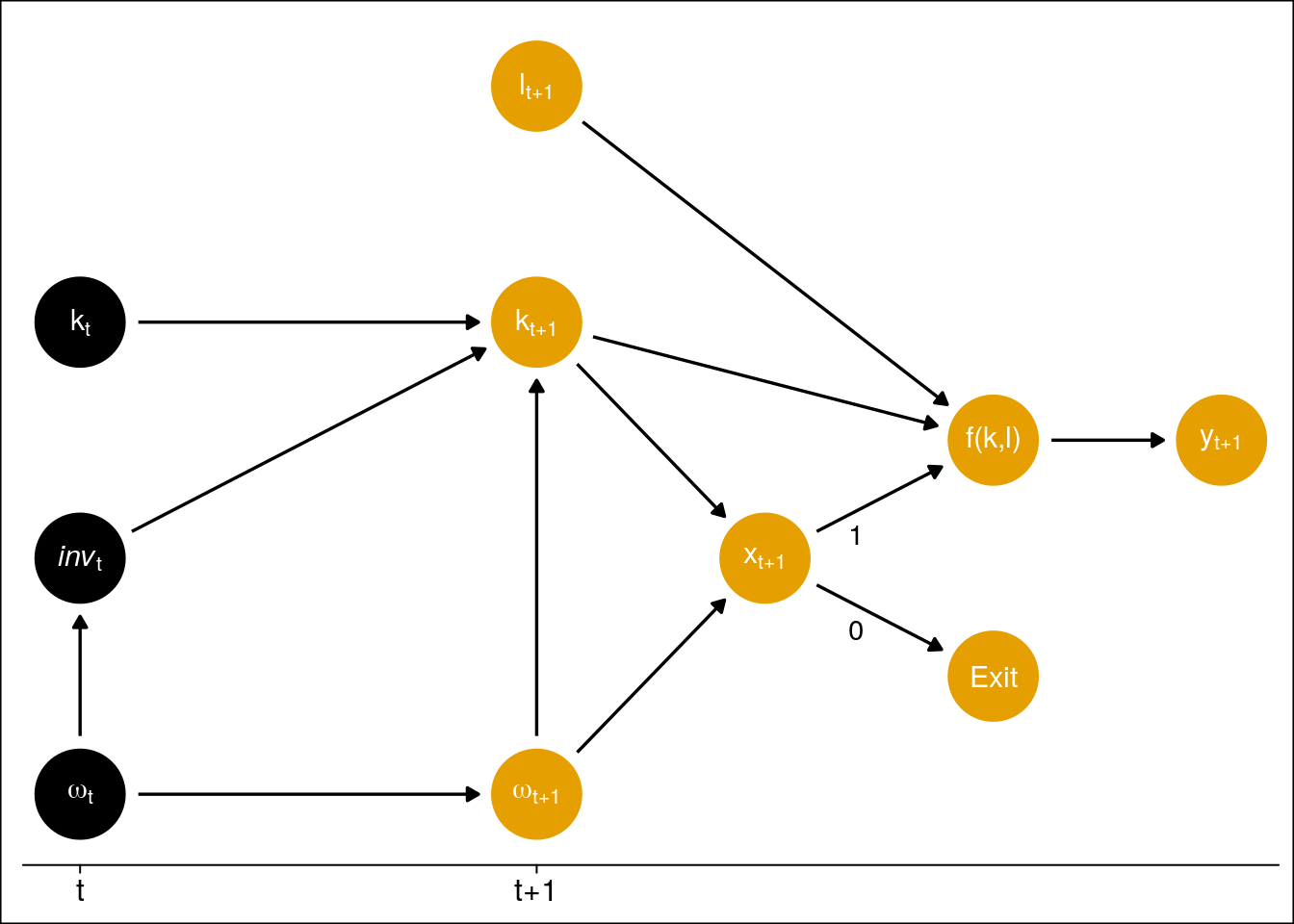
図3.1: OPモデルで仮定した変数の関係
3.5 OPモデルの回帰モデルとしての意味
経営者が (分析者には) 観察されない効果\(\omega_{t}\)を参照して\(k_{t},l_{t}\)を決めてしまうというのは, 計量経済学の文脈でいうなら欠落変数バイアスであり, ここまでで紹介したパネルデータの方法で推定してもバイアスが発生してしまう. さらに \(\omega_{t}\)のマルコフ性を仮定しているため, もし\(\omega_{t}\)が過去の値と相関しているならば, やはり内生性によるバイアスが発生する. また, OPモデルは経営者の撤退という選択肢も想定していることは, サンプルセレクションバイアスを考慮しているとも言える. 前節ではパネルデータには一切欠測がない(バランスドパネル)ことを暗黙の前提としていたが, 実際のパネルデータではしばしば欠測が起こる. もし欠測が企業の活動とは完全に無関係にランダムに発生している(MAR; missing at random)ならば推定に大きな影響はないが, すでに解説したように\(k_{t}\)は\(\omega_{t}\)(の期待値)に相関し, \(\omega_{t}\)の大きさ次第で企業経営者は撤退を決める. つまりモデル内の変数に依存するメカニズムで発生している(MNAR; missing not —)ことになるので推定にバイアスを引き起こす24.
推定のため, 投資を\(\mathit{inv}_{t}=\mathit{inv}(k_{t},\omega_{t})\)という関数で表現できるとして, \(\mathit{inv}_{t}>0\)と仮定すると, 投資関数 \(\mathit{inv}_{t}(\cdot)\)が厳密に単調増加関数であれば25, 逆関数 \(\omega_{t}=h_{t}(k_{t},\mathit{inv}_{t})\) が存在することになる. 言い換えるなら, \(\mathit{inv}_{t}\)は操作変数である. これを(3.2)に代入すると, \[\begin{aligned} y_{t}= & \beta_{L}l_{t}+\left[\beta_{A}+\beta_{K}k_{t}+h_{t}(k_{t},\mathit{inv}_{t})\right]+\varepsilon_{t}\end{aligned}\tag{3.8}\] となり, 観察されない効果を他の説明変数で表現できることがわかった. \(\left[\cdots\right]\)の部分は関数形が特定されていない, いわゆるノンパラメトリックモデルである. しかし, 今知りたいのは\(\beta_{A},\beta_{K},\beta_{L}\)であって, 投資関数を特定することは必須でない. そこで, OP法では以下のような2段階の推定法で一致推定量を得る.
第1段階では\(k_{t}\)と\(\omega_{t}\)という動学的に決定される部分をノンパラメトリック回帰することで, 静学的に決まる\(\beta_{L}\)のみを識別する. そこで, 相関のある部分をまとめて, 以下のように \(\phi_{t}\)と表す. \[\begin{aligned} \phi_{t}(k_{i,t},\mathit{inv}_{i,t}):= & \beta_{A}+\beta_{K}k_{i,t}+h_{t}(k_{i,t},\mathit{inv}_{i,t})\end{aligned}\tag{3.9}\] \(\phi_{t}\)を使うと(3.8)は以下のように書き換えられる. \[\begin{aligned} y_{t}= & \beta_{L}l_{t}+\phi_{t}(k_{t},\mathit{inv}_{t})+\varepsilon_{t}\end{aligned}\tag{3.10}\] このモデルの\(\phi_{t}\)の部分をノンパラメトリック回帰で推定する26ことで, 推定値\(\hat{\beta}_{L}\), \(\hat{\phi}_{t}\)が識別された. これは別の見方をすれば部分線形モデル (partially linear —) である27.
\(\hat{\beta}_{L}\)を得られたので, 当初の式は以下のように書ける. \[\begin{aligned} y_{t}-\hat{\beta}_{L}l_{t}= & \phi_{t}(k_{t},\mathit{inv}_{t})+\varepsilon_{t}\end{aligned}\tag{3.11}\]
よって残りは\(\omega_{t}\)や\(k_{t}\)をひとまとめにした\(\phi_{t}\)からどうやって\(\beta_{A},\beta_{K}\)を識別するかという問題である. ここからがOlleyらの研究の肝であり, 込み入った説明になる箇所である. \(\hat{\phi}_{t}\)には\(\beta_{A}+\beta_{K}k_{t}+\omega_{t}\)が含まれているが, \(k_{t}\)は既に説明したように動学的に決定される. ここで, 次の\(t+1\)時点の \(y_{t+1}-\beta_{L}l_{t+1}\)の期待値を考えると, \(\omega_{t}\)のマルコフ性から以下のように書ける. \[\begin{aligned} \mathrm{E} & \left[y_{t+1}-\beta_{L}l_{t+1}\mid k_{t+1},x_{t+1}=1\right]\\ & =\beta_{A}+\beta_{K}k_{t+1}+\mathrm{E}\left[\omega_{t+1}\mid\omega_{t},x_{t+1}=1\right]\\ & =\beta_{K}k_{t+1}+g(\omega_{t},\underline{\omega}_{t+1})\end{aligned}\] ここで, \(g(\omega_{t},\underline{\omega}_{t+1})=\beta_{A}+\mathrm{E}\left[\omega_{t+1}\mid k_{t+1},x_{t+1}=1\right]\)であり, 欠落バイアスを表している. \(g\)は観測できない\(\omega_{t}\)で構成されるが, (3.7)から, \(t+1\)時点の存続確率\(p_{t+1}\)は\((k_{t+1},\omega_{t})\)の関数で書けることが分かっている. さらに, 期首の\(k_{t+1}\)は前期の\(k_{t},\mathit{inv}_{t}\)に依存する(この\(k_{t+1}\)は\(\omega_{t+1}\)が決まる前の値なので, 経営者が投入量を決めるという話とは無関係). よって, \(t+1\)時点の\(g(\cdot)\)は\(p_{t+1}\)と\(\omega_{t}\)で表現できることがわかる(つまりこれは一種の傾向スコアである).
退出したかどうか(\(x_{t}\))はパネルデータの欠測で知ることができるため, \(x_{t}\) に対してプロビット回帰28をすることで確率の推定値\(\hat{p}_{t}\)を計算できる. さらに, \(\omega_{t}\)は, 第1段階で推定した\(\phi_{t}(k_{t},\mathit{inv}_{t})=\beta_{A}+\beta_{K}k_{t}+\omega_{t}\)から, 以下のように書ける. \[\begin{aligned} \hat{g}(\omega_{t},\underline{\omega}_{t+1})= & g(\hat{p}_{t+1},\hat{\phi}_{t}-\beta_{A}-\beta_{K}k_{t})\end{aligned}\]
\(\hat{g}\)と\(\omega_{t}\)のバイアスを\(\hat{\xi}_{t+1}:=\omega_{t+1}-\hat{g}(\omega_{t},\omega_{t+1})\)として, 当初の式(3.11)に代入できる. 第2段階29では\(\hat{\beta}_{L}\), \(\hat{\phi}_{t}\), \(\hat{p}_{t}\)を所与として, 以下のようなラグのある回帰式を推定する問題として扱える30.
\[\begin{aligned} (y_{t+1}-\hat{\beta}_{L}l_{t+1})= & \beta_{K}k_{t+1}+g(\hat{p}_{t},\hat{\phi}_{t}-\beta_{A}-\beta_{K}k_{t})+\hat{\xi}_{t+1}+\varepsilon_{t+1}\end{aligned}\tag{3.12}\]
(プロビットモデルの推定がバイアスなくできているならば)\(\hat{\xi}_{t+1}\)は平均ゼロでかつ\(k_{t+1}\)とも独立だが, \(l_{t+1}\)とは相関しているかもしれない. しかし\(\beta_{L}\)は第1段階で推定した\(\hat{\beta}_{L}\)を代入できるため, もはや気にする必要はない. \((\hat{\xi}_{t+1}+\varepsilon_{t+1})\)を誤差項とみなすと, \(\beta_{K}\)は誤差項と相関しないので識別できる. そして\(g(\cdot)\)は構造がわからない非線形関数である. そこで, Olleyらは2通りの推定方法を試している. 1つは1段階目と同様に部分線形モデルとしてカーネル回帰を利用する方法, もう1つは, 多項式近似した上で非線形最小二乗法で解く方法である. つまり, \[\begin{aligned} y_{t+1}-\hat{\beta}_{L}l_{t+1}= & \beta_{K}k_{t+1}+\sum_{d=1}^{q}\sum_{m=0}^{d}\gamma_{m,d-m}\hat{h}_{t}^{m}\hat{p}_{t}^{d-m}+(\hat{\xi}_{t+1}+\varepsilon_{t+1})\end{aligned}\] である. ここで, \(\hat{h}_{t}:=\hat{\phi}_{t}-\beta_{A}-\beta_{K}k_{t}\)で, \(q\)は多項式の次数である. なお, OP法では標準誤差を代数的に得られないため, ブートストラップシミュレーションで計算する必要がある. この方法で導出したモデルの統計的性質は Pakes and Olley (1995) でより詳しく説明されている.
3.6 モデルの事後診断
さて, 反事実分析でのモデルの評価は単に当てはまりが良いかだけでなく, 仮定と現実のデータが矛盾していないかの確認も同等かそれ以上に重要である (今回は研究のアイディアとRの実装を紹介するのが目的なのでこの工程は省く).
ここでもOlleyらの研究を例にする. まず, 彼らの仮定が正しければ, 単なる最小二乗法や, IVなどの方法では結果にバイアスが発生するはずである. よって, 提案する推定方法との比較が必要である. あるいは, サンプルセレクションバイアスが実際に発生しているか確認するため, バランスドパネルでの結果と比較することも必要である. さらに, 市場の構造は法規制の変化によって変わりうる. 法改正のタイミングで年代ごとに区切って当てはまりを確認する必要がある.
さらに, モデルのロバストネス分析として, モデルの仮定のうち特に重要な, 投資関数の式(3.6)を検討している. 投資が資本と観察できない生産性によって決まるという仮定が正しくない場合, \(\beta_{L}\)の推定にバイアスが生じる. これを検証するには最後の式(3.12)の説明変数に, 現在の\(l_{t}\)を加えることでできる (このようなタイプの検証は特定化のテストと呼ばれる).
References
Ackerberg, Daniel A., Kevin Caves, and Garth Frazer. 2015. “Identification Properties of Recent Production Function Estimators.” Econometrica 83 (6): 2411–51. https://doi.org/10.3982/ECTA13408.
Anderson, T. W., and Cheng Hsiao. 1981. “Estimation of Dynamic Models with Error Components.” Journal of the American Statistical Association 76 (375): 598–606. https://doi.org/10.1080/01621459.1981.10477691.
Anderson, T. 1982. “Formulation and Estimation of Dynamic Models Using Panel Data.” Journal of Econometrics 18 (1): 47–82. https://doi.org/10.1016/0304-4076(82)90095-1.
Arellano, Manuel, and Stephen Bond. 1991. “Some Tests of Specification for Panel Data: Monte Carlo Evidence and an Application to Employment Equations.” The Review of Economic Studies 58 (2): 277. https://doi.org/10.2307/2297968.
Blundell, R, and Steven Bond. 1998. “Initial Conditions and Moment Restrictions in Dynamic Panel Data Models.” Journal of Econometrics 87 (1): 115–43. https://doi.org/10.1016/S0304-4076(98)00009-8.
Levinsohn, James, and Amil Petrin. 2003. “Estimating Production Functions Using Inputs to Control for Unobservables.” Review of Economic Studies 70 (2): 317–41. https://doi.org/10.1111/1467-937X.00246.
Mairesse, Jacques. 1990. “Time-Series and Cross-Sectional Estimates on Panel Data: Why Are They Different and Why Should They Be Equal?” In Panel Data and Labor Market Studies, edited by Joop Hartog, Geert Ridder, and Jules Theeuwes, 81–95. North-Holland: Elsevier Science Publishers B.V.
Olley, G. Steven, and Ariel Pakes. 1996. “The Dynamics of Productivity in the Telecommunications Equipment Industry.” Econometrica 64 (6): 1263–97. https://doi.org/10.2307/2171831.
Pakes, Ariel, and Steven Olley. 1995. “A Limit Theorem for a Smooth Class of Semiparametric Estimators.” Journal of Econometrics 65 (1): 295–332. https://doi.org/10.1016/0304-4076(94)01605-Y.
Wooldridge, Jeffrey M. 2010. Econometric Analysis of Cross Section and Panel Data. 2nd ed. The MIT Press. https://mitpress.mit.edu/books/econometric-analysis-cross-section-and-panel-data.
奥井, 亮. 2016. “動学的パネルデータモデル.” http://www.sigmath.es.osaka-u.ac.jp/~Estat/h28_datascience2/okui_handai28_v2.pdf.
こういった初歩的な話は, 私なんかよりよほど深く理解した大学の先生がいくつも教科書を書いており, 正確さや詳しさでそちらのほうが遥かに良い. 参考文献には一般公開されている 奥井 (2016) のスライド, Wooldridge (2010), Ch. 10-11 の教科書などがある. 私はほぼWooldridgeの教科書で勉強したため, 日本語の教科書に詳しくない……↩
TFPの計測方法やその批判についてはググれば内閣府とか日銀とか経済産業研究所 (RIETI) の公開している日本語の論文がたくさん引っかかるので適当に勉強すれば良いだろう.↩
ただし, 一致するのは期待値のみで, 標準誤差の計算方法は変わる. 仮説検定・区間推定をするならば clustering-robsutな標準誤差と呼ばれるものを使う.↩
逆に観測されない効果が時間ごとに異なるが, 企業間では一定の場合も同じようにできるだろう. その場合はグループ間 (between) 推定量と呼ばれる.↩
久保 (2012) は生物学の文脈で異質効果のある場合の解法として一般化線形混合モデル(GLMM)を紹介している. これは観測されない効果の問題とよく似ている. 生物の実験データではおそらく変数との相関がないため, 定数項のバイアスと, 当てはまりの良さだけが問題となるのだろう. GLMMは誤差分布が正規分布と異なる場合も考えているが, パネルデータは線形モデルを基本として議論を進めることが多い.↩
古い本なので大学図書館などでないと閲覧が難しそうだ. 私も手元にないので学生の頃に書いたメモを元に書いている. また, 川口先生の講義ノートではこのあたりの問題に関する参考文献として Griliches and Mairesse (1999) を挙げている. タイトルからしてもこちらのほうがカバー範囲の広いサーベイのようなので, こちらを参照したほうがいいのかもしれない.↩
GMMも以前ブログに定義を書いたが, 詳しいことは Hayashi (2000), また, 他の教科書として動学パネルデータを重点的に解説した 千木良, 早川, and 山本 (2011) などがある. Baltagi の教科書も授業でおすすめされていた気がするが私は読んでいないのでどこまで書いてあるか知らない. どうしても本を買いたくない/買えない人 奥井 (2016) の講義スライドを見ると良い.↩
より正確には, Olleyらは工場単位でのデータを利用しているため彼らが推定したのは工場単位での生産関数である.↩
日本語では, たとえば北村, 西脇, & 村尾 (2009, 不完全資本市場下での生産関数の推定について)が理論的根拠を詳しく解説している. 彼らの解説で使われているのは本来のものに加えて原材料費や純資産を考慮したモデルだが, 本質的な部分は変わらない. 統計モデルとしての説明なら彼らのものでも十分だが, 今回は経済モデルとの関係を強調したいため, あえてOlleyらの論文をなぞって冗長に書いておく.↩
Olleyらの当初の仮定では, 企業年齢も生産性に影響があると考えていたが, 実際に推定してみるとほとんど影響がないことがわかった. モデルの特徴を説明する上でも企業年齢はあまり関与しないため, ここでは省略している.↩
これをベルマンの最適性原理という. しかしこれ以降の動学最適化問題の数理的に厳密な話をしていてはキリがないので, 適当な参考文献に投げることにする. ただし私は動学最適化を純粋に数理的側面で説明した教科書を読んだことはなく, 経済学の文脈で主に勉強しているので, 挙げる参考文献も必然的にそういうものになる. 日本語文献でかつ無料で一般公開されているものとしては, マクロ経済学での応用の観点で書かれた工藤 (2007, 動学的最適化入門), 阿部 (2017, 上級マクロ経済学 講義ノート 動的計画法), 蓮見 (2019, 動学マクロ経済学入門)の講義ノートがある. 教科書ではA.C. Chang の『動学的最適化の基礎』の邦訳は比較的簡単に解説しているが誤植が多いことで有名である. 西村清彦の『経済学のための最適化理論入門 』という教科書もあるが, どこまでカバーしていたかの記憶が定かではない. もっとも詳しいのはやはりStokey, Lucas, & Prescott (1989, Recursive methods in economic dynamics), Ljungqvist & Sargent (2018, Recursive macroeconomic theory)の教科書あたりか? 単に「ベルマン方程式」でググると強化学習に関連するものとして言及する記事がよく引っかかるが, これらはベルマン方程式というより分枝限定法の考え方の解説だったり, 内容がメモ程度の断片的だったりするので今回の話の補足説明には向かない. 理論モデルでは連続時間を想定する場合もあり, ベルマン方程式の代わりに Hamilton-Jacobi-Bellman方程式を応用することもある. こちらは物理学でもよく使われるようだ.↩
元の論文では時間インデックスをずらして\(p_{t}:=\mathrm{P}(x_{t+1}=1\mid\cdots)\)としていることに注意.↩
欠測が推定結果に及ぼす影響については, 星野 (2009), 高井, 星野, and 野間 (2016), 高橋 and 渡辺 (2017) のいずれかが参考になるだろう. ただしパネルデータでの問題については星野が少し触れている程度である. 英語でもいいならば Wooldridge (2010), Ch. 19 が解説している.↩
\(k_{t}\)に対して単調増加である理由はすでに示唆した. 一方で\(\omega_{t}\)が大きければ, 経営者はやはり将来の利益が大きくなると予測し, 設備投資を増やす傾向にある, という理由でこの仮定を説明できる. しかし現実のデータがこの仮定を満たすとは限らない. 実際には規模縮小のために資産を売却するという選択肢もあり, このとき設備投資はマイナス扱いになる. しかしこの仮定はかなり強い仮定であり, これ以降も Levinsohn and Petrin (2003) などがこの仮定がもたらす問題が取り上げられている.↩
Olleyらは4次の多項式補間で計算しているが, これは次数を増やしてMSEおよび係数が変化しなくなるものを採用するというルールで推定したためである. 一方で, 年代で分割して試すと変化が見られたとしている. 多項式に特定する理由もないので, 部分線形モデルはカーネル平滑化による計算も可能だが, こちらは次元が増えると計算に時間がかかるという性質がある.↩
特定のパラメータだけを推定するために, 操作変数の式を与えて内生性によるバイアスを排除する方法をコントロール関数アプローチという. Cameron and Trivedi (2005), Wooldridge (2010) にもコントロール関数の解説があるが, 日本語の教科書では見た記憶がない. ググってもコントロール関数のアイディアを解説しているのは明城 (2012, 製品差別化財の需要関数推定における内生問題について)くらいで, それも需要関数推定の問題に限定したものなので少しわかりにくいかもしれない. 解説したものは私が以前自分で書いたものくらいしかない (これもあまりおすすめできない). Kawaguchiが部分線形モデルでの応用に関して参考文献として挙げるToddとIchimuraの論文はHandbook of Econometricsに収録されているので研究機関に所属していない人間がアクセスするのは少し大変である. 代わりに Blundell and Powell (2003) ならば一般公開されている.↩
Olleyらはこれも1段階目の推定と同様の方法で次数を決めた多項式展開でプロビット回帰をしている.↩
Olleyらの論文では\(p_{t}\)の推定を第2段階と呼んでいるので, これは原文では第3段階である. しかし後の解説では省略されることが多い.↩
スライドでは余白節約のため(3.12)を \(\hat{\omega}_{t}:=\hat{\phi}-\beta_{A}-\beta_{K}k_{t}\),\(e_{t+1}:=\hat{\xi}_{t}+\varepsilon_{t+1}\)と置き換えて表現している.↩