4 R での実装
4.1 データのとり方
企業の生産関数推定で一番むずかしいのは実はここかもしれない. というのも, 理論上の\(K\)や\(L\)はどこにも記載されていないからだ. これはけっこう地道な計算が必要になる. 例えば企業の決算報告書などから地道に計算する, あるいは日銀やDBJのような政策金融機関が整備しているデータベースをなんらかの手段で見せてもらう, などである. あるいは, 農業や工業など資源と生産物の関係が分かりやすい特定の産業だけでを分析の対象とすることもできる. 例えば農業で, \(K\)を乳牛の頭数, 原材料を飼料, \(Y\)をミルクの生産量とした分析も可能だろう (昔見た気がするがすぐには見つけられなかった). 今回はとてもそんなことをしている暇も金もコネもないので31, 後述する乱数データを使う.
estprodパッケージが, Olley-PakesやLevinsohn-Petrinの方法を実装したという. さらに, このパッケージには練習用の乱数データセットも用意されている.
この乱数がどのような方法で生成されたかがわからないので, 実質的に動作確認にしかならないが, まずはこれを使ってみた. しかし, 1段階目の推定を検証してみたところ, 残差プロットの形がかなり変になった. 残差プロットが必ず完璧な45度線を引かなけばならない, ということはないが, データの生成方法は分からないこともあって用例として不安である32. よって, Kawaguchi (2019) の課題2に沿って疑似データを生成してやり直すことにした.
しかし, 去年の講義内容とはいえ課題の答案を勝手に一般公開してしまうのも無配慮すぎる気がするため, 乱数データを作成するプログラムは非公開として, 当初の課題から乱数シード値などを変更して作成したデータdf_sample, df_ground_truthのみ公開する. 前者は標本データで, 後者は\(\omega_{t},p_{t}\)など本来は観測できない変数も見えるようにしたデータである(表4.1, 以下, 後者を「正解データ」と呼ぶ). 以降はこのdf_sampleを使ってパラメータを推定する. 推定したい3つのパラメータは元の課題どおり,
\(\beta_{A}=1,\beta_{K}=0.7,\beta_{L}=0.2\)としている.
i |
t |
k |
k_lag |
inv |
inv_lag |
x |
y |
y_true |
omega |
p_x |
|
|---|---|---|---|---|---|---|---|---|---|---|---|
| 標本 | 企業ID | \(t\) | \(k_{t}\) | \(k_{t-1}\) | \(\mathit{inv}_{t}\) | \(\mathit{inv}_{t-1}\) | \(x_{t}\) | \(y_{t}\) | NA | NA | NA |
| 正解データ | 企業ID | \(t\) | \(k_{t}\) | \(k_{t-1}\) | \(\mathit{inv}_{t}\) | \(\mathit{inv}_{t-1}\) | \(x_{t}\) | \(y_{t}\) | 退出しない場合の\(y_{t}\) | \(\omega_{t}\) | \(p_{t}\) |
なお, 乱数生成したため, 偶然にも一部の企業が全期間で退出している. データとして不自然だが計算には問題ないので修正せずそのままにしている.
4.2 \(\beta_{L},\phi\)の識別
1段階目の推定は部分線形カーネル回帰で推定する. これはnpパッケージで提供されている. 今回はnpplregbw()でデータから最適バンド幅を決定し, 決定したバンド幅をnpplreg()に与えて推定する3334. この推定結果を残差プロット等で確認したら, \(p_{t}\)の推定を行う. 1段階目のモデル(3.10)は, 誤差項と相関のある部分線形モデルであり, 単に多項式やスプライン近似を適用しただけでは正しく\(\phi\)を推定できないため, npplregbw(formula = y ~ l k + inv)としても誤差項の相関のために\(\beta_{L}\)は正しく推定されず, 全く異なる値になる. そこで部分線形モデルとコントロール関数アプローチの併用によって\(\beta_{L},\phi\)を識別する. このためには, formula = y ~ l + k | k + inv と指定する. これで, \(\beta_{L},\phi\)を識別できるが, もちろんこの時点では \(\beta_{K}\)は正しく推定できていない.
# somehow `na.action` doesn't work so we need `drop_na()`
bw_1st <- npplregbw(formula = y ~ l | k + inv, data = df_sample %>% drop_na(y, k, l, inv))
fit_1st_np <- npplreg(bw_1st)
summary(fit_1st_np)なお, npパッケージのノンパラメトリック回帰は計算負荷がけっこうある. そこで, 面倒だったらOlleyらと同様に以下のような多項式近似でごまかしても良い.
degree = q は多項式の次数で, formulaを評価する際には\(\sum_{r\leq q}k_{t}^{r}\mathit{inv}_{t}^{q-r}\) と認識される. 何も考えずに degree = 4 としてもそこそこそれらしい値を推定できるが35, Olleyのやるように推定値とMSEが安定する次数を選ぶのがスマートだろう. しかし残念ながら stats::step() 関数には poly() の次数を調整する機能がないので, ループ処理か予め決めた次数までを並列処理して比較する必要がある. そこで, 以下のように10次までの多項式あてはめを一度に実行する処理を書いた36.
set.seed(42)
df_fit_1st_poly <- tibble(q= 1:10) %>%
mutate(model = map(q, function(q){
if(q == 1){
poly_term <- "+ k"
} else{
poly_term <- paste("+ poly(k, inv, degree =", q, ")")
}
lm(as.formula(paste("y ~ 1 + l + k", poly_term )), data = df_sample)
})) %>%
mutate(
rmse = map_dbl(model, function(x) sqrt(mean(x$residuals^2))),
coef = map(model, function(x) enframe(coef(x)) %>% filter(name %in% c("k", "l")))
) %>% unnest(coef) %>% pivot_wider(names_from = name, values_from = value)
# we select 5th order, the estimate of beta_l = .161
fit_1st_poly <- df_fit_1st_poly$model[[5]]ところで, 現在はノンパラメトリックな回帰モデルとしてスプライン回帰の研究が進んでいる(基本的な事項は Hastie, Tibshriani, and Friedman (2009), Ch. 5), 坂本, 井筒, and 白旗 (2009) などを参照). スプライン回帰にもバリエーションがあるが, 典型的なものは区間ごとに異なる次数の多項式で表現するため,
単純な多項式近似よりも表現の自由度の高い非線形近似の方法である. さらにSemiPar::spm()は部分線形モデルに対しても罰則付き最尤推定という方法で当てはめたスプライン回帰を計算することができる. 表現の自由度で言えばカーネル回帰のほうがさらに優れているが, 計算時間はこちらのほうが少ない. 多項式近似である程度うまくいくのだからスプライン回帰でもうまくいくと思ったのだが, なぜかうまく行かない. 原因を調べるのがめんどくさくなったので読者の課題とする.
4.3 存続確率の推定
Olleyは, 理論モデルの仮定から\(p_{t+1}\)を決定する関数は\(k_{t},\mathit{inv}_{t}\)の2変数関数で表現できることから, この2変数を使ったプロビットモデル(ロジットリンク関数を標準正規分布に置き換えたもの)と多項式近似またはカーネル回帰を組み合わせて確率を推定している.
今回は正解が分かっているため, \(p_{t+1}\)と\(k_{t},\mathit{inv}_{t}\)の関係を知ることができる. 2変数の散布図とカーネル回帰で近似曲線を当てはめたものが以下のようになる. プロビットモデルならば, \(p_{t+1}\)を標準正規分布の逆分布関数 (分位点関数)で変換した値と説明変数が線形相関していれば, その説明変数を使うことで当てはまりの良いモデルができると予想できる. しかし, 図4.1からわかるように, 2つの説明変数との相関関係はいずれもあまり直線的でないことがわかる.
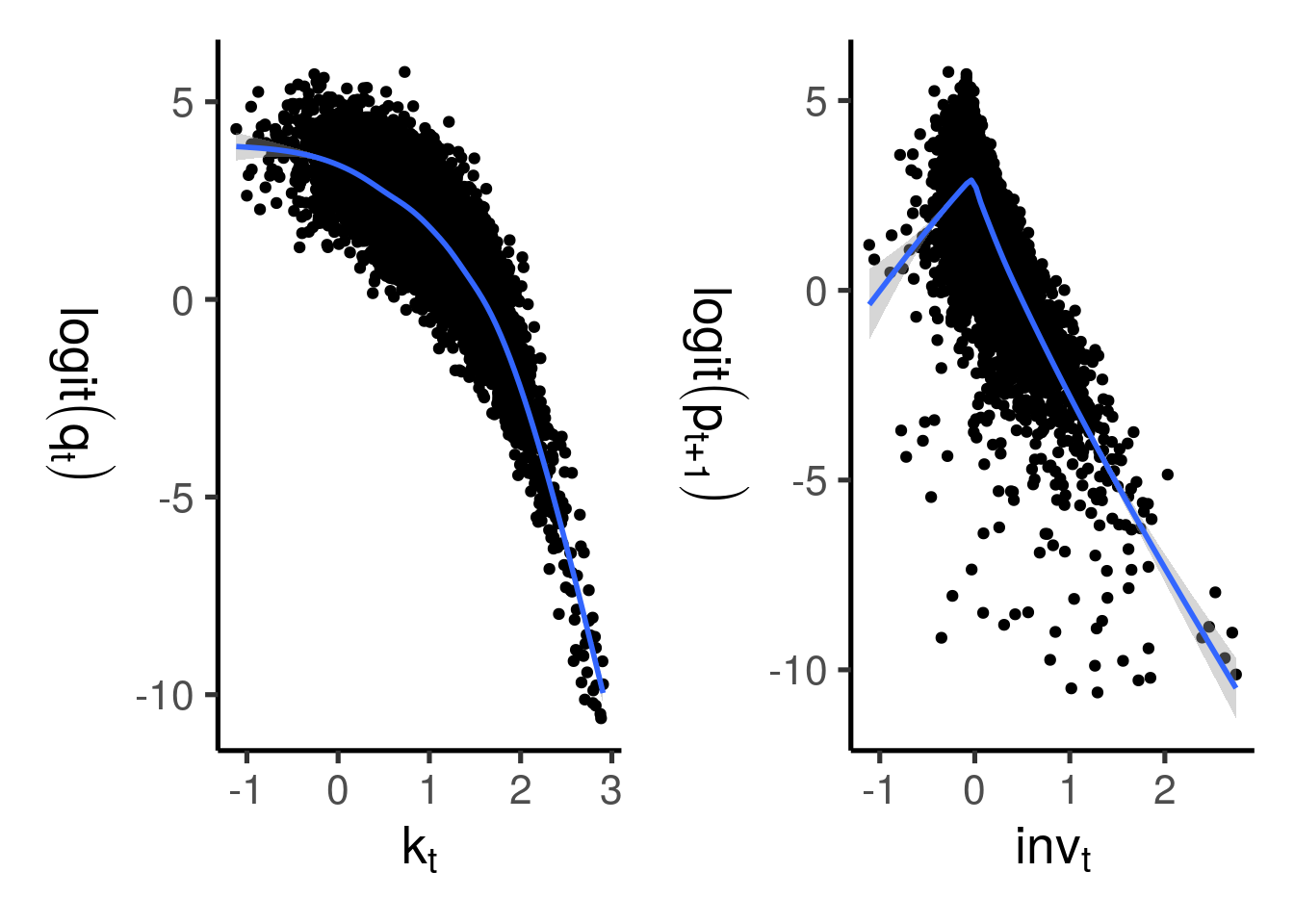
図4.1: 真の確率と説明変数の相関
よって, 単なる一般化線形回帰ではなく, より複雑な非線形近似方法を使う必要があるとわかる. Rでは多項式プロビット回帰はglm()とpoly()の組み合わせで,
例えば以下のようにして計算できる. ここでも次数をデータの当てはまりで決定するため\(\beta_L\)の推定と同様に次数を変えて並列処理している.
1段階目で使用したnpパッケージは線形回帰のみ対応しているため, プロビットモデルの推定はできない. 他のRのパッケージでは,
例えば各変数をスプライン補間などで非線形変換した一般化加法的モデル (GAM37)を計算できるmgcvパッケージ, 一般化ガウシアンカーネル回帰のできるbkmrパッケージや, 一般化部分線形モデルを計算できるgplmなどがある. これらはいずれもノンパラメトリックあるいはセミパラメトリックなモデルと呼ばれるが, それぞれ表現方法が違うため, 当てはまりの良さも変わってくる38. また, このパートではそもそも係数の推定が不要なので, 確率さえ推定できているならランダムフォレストのような自由度の高いモデルでも問題ないだろう39. 今回はmgcv, bkmr, gplm, rangerなどを使って推定してみた.
なおKawaguchiの課題では退出行動を省略しているのでこのパートは存在しない.
4.4 \(\beta_{A},\beta_{K}\)の推定
最後の推定は, \(\omega_{t}\)を推定し, さらに企業の退出行動によるサンプルセレクションバイアスを補正するための計算である.
まず, 計算の無駄をなくすためにの関数のように推定に必要なラグ項をデータフレーム側で作成しておく. mutate()関数内でdplyr::lag()を使えばそれぞれのラグ項を得られる40. 元のパネルデータをdf_sample, 1段階目の推定結果をfit_1stとして, 2段階目の推定のためのデータセットdf_sample_2ndを作成している.
y_bl, phi, p_x はそれぞれ\(y_{t}-\hat{\beta}_{L}l_{t},\hat{\phi}_{t},p_{t}\)に対応する.
make_2nd_sample <- function(data, beta_l, phi, p_x){
data %>%
mutate(
bl = l * beta_l * l,
y_bl = y - bl,
phi = phi,
p_x = p_x
) %>%
arrange(i, t) %>% group_by(i) %>% mutate(
phi_lag = lag(phi),
) %>% ungroup
}ここで一旦, 実際には観測できない \(\beta_{L},\omega_{t}\)の情報を使って\(\beta_{K}\)を正しく推定できることを確認してみる. 以下のように\(y_{t}-\beta_{L}l_{t}-\omega_{t}\)に対して線形回帰をした結果, \(\beta_{A}=1.00,\beta_{K}=0.70\)とほぼ正確な値が出ている.
| Estimate | Std. Error | t value | Pr(>|t|) | |
|---|---|---|---|---|
| (Intercept) | 0.851 | 0.008 | 112.044 | 0 |
| k | 0.700 | 0.008 | 88.000 | 0 |
しかし, 実際には\(\omega_{t}\)は不明であり, 1段階目で推定した\(h_{t}\)と確率\(p_{t}\)から推定する41. Olleyらの方法と同様に多項式近似による非線形最小二乗法で計算する.
なお再び正解データを覗き見すると, \(\hat{\phi}_{t},\hat{p}_{t+1}\)と\(\omega_{t+1}\)の関係はそれぞれ図4.2のようになっている.
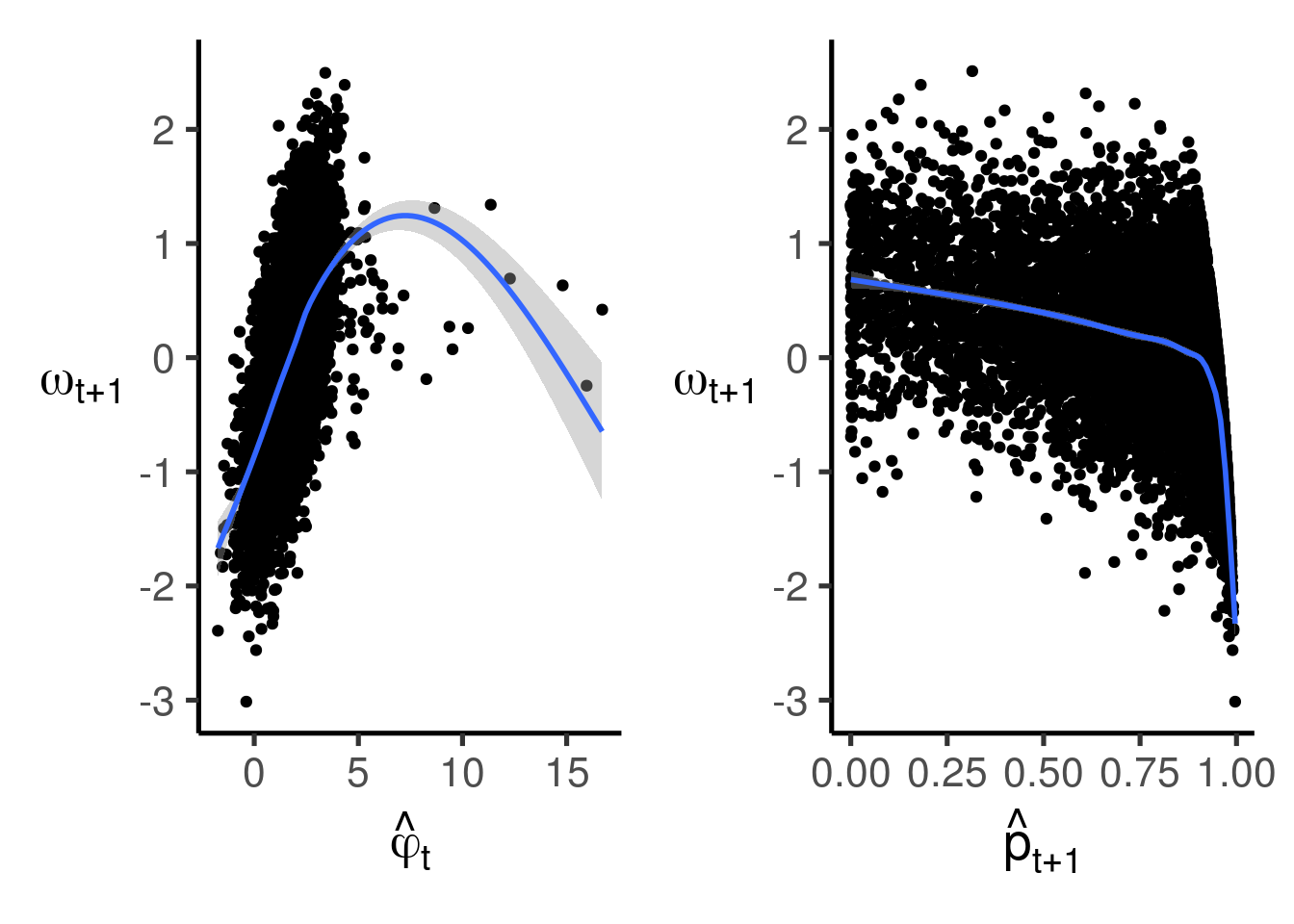
図4.2: \(\hat{\phi}_{t},\hat{p}_{t+1}\)と\(\omega_{t+1}\)の正解データとの相関関係
非線形最小二乗法の計算はstats::nls()関数が提供されており, この関数はformulaで記述できたり, lm()のように標準誤差を計算してくれたりする. しかし今回は多項式部分をformulaで記述するのがやや面倒なのと, nls()の計算する標準誤差が意味をなさないため, optim()関数で計算する. 目的関数は以下のように, 任意の次数の(3.12)のMSEを計算できるような関数を作った.
\(p_{t},h_{t}\)の交差項を含む\(q\)次多項式の第\(d\)次項は\(d+1\)個存在するため, 1次から\(d-1\)次までの項の総数は\(\sum_{i=1}^{d}i\), 項の総数は\(\sum_{d=1}^{q}(d+1)\)個であるから, 上記のようにpurrr::map_dfc(), purrr::reduce()を入れ子にして計算した42. なお, 数値計算上の観点から初期値にも注意する必要がある. これは補遺Aで詳しく説明している. また, Olleyらはさらにここでもカーネル回帰も試しているが, パラメータが含まれる非線形式のカーネル回帰は自分で1から書かなければならず面倒になったので今回は省略する.
そして標準誤差を代わりに (ノンパラメトリック) ブートストラップ法で計算する. ブートストラップ法による標準誤差の計算方法は補遺Bで補足説明している.
以上で説明した内容は, Githubリポジトリのall_public.Rにまとめてある.
References
Hastie, Trevor, Robert Tibshriani, and Jerome Friedman. 2009. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. 2nd ed. Springer. https://web.stanford.edu/~hastie/ElemStatLearn/.
Kawaguchi, Kohei. 2019. “ECON 6120I Topics in Empirical Industrial Organization.” https://kohei-kawaguchi.github.io/EmpiricalIO/.
坂本, 亘, 井筒理人, and 白旗慎吾. 2009. “罰則付きスプラインによる非線形回帰構造の推測.” 計算機統計学 21 (1-2): 55–94. https://doi.org/10.20551/jscswabun.21.1-2_55.
いくつかの計量経済学の教科書の著者は練習問題用にデータセットを公開している. 例えば Wooldridge data sets, Datasets for empirical exercises in Econometrics など. しかし, 今回の問題に適した企業別パネルデータは見つけられなかった.↩
このパッケージはCRANに登録されているものの, 作者のプロフィールがよくわからない. また, githubリポジトリにもほとんど関心が集まっていないため, 動作がどの程度適切なのかあまり確認が進んでいなさそうだ. あと,
coefs(),predict(), といったstatsの基本関数にも対応していない. もちろんstargazerに対応していないし,estimatrにも収録されていない. 他にも, 企業退出を考慮しているように見えて実は不均衡パネルデータを想定した実装になっていないなどの問題があった.↩Olleyら本来のやり方を踏襲するなら, 時点ごとに分けて当てはめるのが正統だが, 今回はプール推定する.↩
なお,
npパッケージに与えるデータをtibbleで与えるとエラーが出る(しかも一見関係ないメッセージ)ので注意する. また, デフォルト設定であるna.action = stats::na.omitで欠損値を含むレコードを除外して計算するはずだが, なぜか機能しない. そのため入力データから欠損値を除外する処理を自分で書かなければならない.↩今回これでもうまくいくのは, データの生成過程が単純だからである. 実際のデータに応用するときは, データの特性, つまりどういう現象から取得したデータなのかをよく考えて方法を柔軟に変えねばならない.↩
estimatrやtidymodelsなどならもっと簡単に書けないかとも考えたが, これらのパッケージは今回使う推定方法に意外と対応していない.↩参考: Hastie, Tibshriani, and Friedman (2009), Ch. 9), 鈴木大慈の講義スライド, あるいは言語研究者からの観点だが『GLMM/GA(M)Mの文献案内』で挙げられているリストも興味深い. また, 以前紹介したprophetのモデルも一般化加法的モデルの一種である.↩
この場でこういったノンパラメトリック回帰の方法まで細かく説明するのは面倒なのでしない. GAMやカーネル回帰はとりあえず Hastie, Tibshriani, and Friedman (2009), ch. 5 の教科書を読んで欲しい. または Li and Racine (2007) の教科書か. それ以外の細かい話は各パッケージのマニュアルで参照されている論文を読んでほしい.↩
plmとstatsにもlag()関数があるが, こちらはmutate()内で使用しても評価されないし, エラーも発生しないため, 呼び出し順に注意. あるいはconflictedパッケージも併用すると良いだろう. このパッケージの解説は『名前空間の衝突をconflictedパッケージで防ぐ』でなされている.↩欠測メカニズムが分かっている場合, セレクションバイアスを補正するHeckmanの選択モデル (Heckit, or Type-II Tobit)モデルが応用できる場合がある. しかし今回は欠測確率\(p_{t}\)が\(k_{t}\)に影響して決まるため, Heckitは意味をなさない.↩
実際にはこういう複雑な計算に出くわしたら何も考えずに
rcppに切り替えてfor文で書いたほうが効率が良い気もする.↩