2 イントロダクション
2.1 構造推定とは
では構造推定とは何だろうか. 構造推定で検索すると, 名前が似ているが違うものがいくつか出てくる.
2.1.1 構造方程式モデリング
例えば構造方程式モデル(SEM)というものがある. これは変数間の関係構造を同時線形方程式で表したもので, 因果推論のフレームワークの原型ともいえるものだが, 構造推定とは違う.
2.1.2 構造時系列モデル
構造ベクトル自己回帰モデル (Structural VAR) とか, ベイズ構造時系列モデル (BSTS) というものがある.
通常のVARは複数の変数の時系列変化を扱うモデルで, それぞれの変数が過去の値にのみ依存して決まる回帰モデルなのに対して, 構造VARは現在の別の変数にも依存する, 同時決定的な時系列モデルである1. ベイズ構造時系列モデルの「構造時系列」はHarveyのいう構造時系列モデルのことを指す(Scott and Varian 2014). これは89年とかなり古い教科書なので私も読んだことがないが, Lütkepohl (2007), p. 618によればローカルトレンドモデルを基本とした時系列モデルらしいので, 多変量時系列モデルというわけでもなく, 状態空間モデルに属する. これらも構造推定とは関係ない.
2.1.3 構造型モデル
いちおう過去のTokyo.Rの発表ネタとかぶらないか確認したところ, こんなものを見つけた.
「構造型モデル」という名前も構造推定と似ている. いちおう元になった Merton (1974) の論文も確認した. しかしこれも構造推定ではない.
構造推定の定義について, 多くの人は Reiss and Wolak (2007) を挙げるが, この本はとにかく分厚くて高いので私は持っていない. 前回で触れたように,観察されたデータにそのまま回帰式や他の関数を当てはめても因果関係を知ることはできない. そこで, いくつかの要素が必要になる. そこで構造推定は仮定によって構造を特定しようとした.
北村 (2016, 応用ミクロ計量経済学の手法と論点)は一般的な型はないとしつつ, その解説を要約すると3つの特徴があるとしている.
経済理論モデルであること
確率モデルであること
データに基づいて推定されていること
(1)はいわゆるルーカス批判 Lucas (1976) を受けて, 彼の批判を克服できるような経済理論に基づいたモデルづくりを意識するようになった. (2)はちょっとわかりづらい. 回帰分析だって正規分布を暗に仮定しているから確率モデルになる. しかしここでは, 観察できないものと, できるものの不確実性を考慮しているという意味である. 例えば測定誤差や, 分析者には観測できないが, 経済活動の当事者は知っている情報というものがある. これらを無視した推定はしばしばバイアスを引き起こすが, 構造推定ではモデルにこのような仮定を取り込む. (3) は, 完全な架空の話ではなく, なるべく現実と整合するために観測されたデータに基づいてパラメータを決定するということである.
よって, 最初に挙げた「構造方程式モデリング」や「Mertonの構造型モデル」は経済理論に基づいた構造を表現していないため構造推定ではない. ただし構造時系列モデルは, 実は80年代にマクロ経済モデルとして利用された歴史がある. 経済理論に基づかないという批判は当時からあったものの, 単に予測するだけなら問題ないということで使われていた. しかし, 「どうなるか」と「なぜそうなるのか」のどちらを求めているかと言えば前者であり, 原因を分析することはできない2.
一般に定まった方法はないが, かといって完全な無手勝流ではない. 大学院のコアコースで教えるモデルはだいたい決まっており, 多くの研究も先行研究のフレームワークを応用していることが多い.
2.2 因果推論と何が違うのか
以前にも紹介したようなRCT, 準実験(操作変数法, 傾向スコア法, DID, RDD) なども, 「反事実的な因果推論」と呼ばれる. しかしこれらは経済学の理論仮説に基づく因果関係ではなく, ランダム化と比較によって「平均処置効果」を求めるフレームワークである3. 一方で構造推定は実際のデータと理論モデルを融合させた結果なので, 本来の意味で現実には起こり得なかったこと (反事実) を推論するフレームワークである.
具体例を挙げよう. 今回は経済学における生産関数の推定の例を紹介する. 原材料を投入し, 財を生産する, その変換ルールを関数に表したものを生産関数という. 例えば, 資本(\(K\)apital4)と労働力(\(L\)abor force), \(Y\)は出力, つまり生産量なので, 生産関数を以下のように表せる
\[\begin{aligned} Y= & F(K,L)\end{aligned}\]
この生産関数の形状が分かれば,
実際のデータとの残差から, 数値に表れない生産性 (TFP) を計測する (残差分析)
もし設備投資を増やしたら (\(K\)を増加させたら) どれくらい生産量が増えるか
もしパラメータが変化したら, 生産力はどう変化するか (比較静学分析)
と言ったことがわかる.経済学部出身者ならば, ミクロ経済学の授業で聞いた覚えがあるだろう. しかし, データから推定した係数が「もし変わったら」というのは, 本質的に現実に起こっていない事象について話していることになる. 同等のことを因果推論でやるとすれば, 両方のケースについて実際に観測したデータに基づいて差を比較しなければならない. つまり, 単にデータを近似しただけの関数では, これらのことを言う根拠として弱い.
経済学ではRCTや準実験アプローチは誘導形 (reduced form) 推定5とも呼ばれ, 構造推定派と誘導形推定派は数年前までお互い相手のアプローチの問題点を指摘し激しく論争していた. その結果, 現在ではそれぞれのアプローチでできることの限界がはっきりしてきたため, 論争というほどのことはない6.
両者の使い分けとしては, 構造推定は経済理論モデルというある意味「架空のもの」に基づいて未来に起こりうることについての分析もできるが, 因果推論は実態としては実験計画法と本質的に同じで統計学の理論に基づいて観察できたデータから事後評価するアプローチである. よってしばしば, 構造推定は反事実(反実仮想)シミュレーション7, 因果推論はプログラム(政策)評価とか介入(intervention)といって呼び分けられる8. そして構造推定は理論仮説に強く依存したフレームワークであるので, 仮説が妥当なのかはよく注意が必要である. ただし, かといって因果推論が仮定に依存しないというのも完全な誤りである. 前回でも言及したが, 因果推論であっても必ず仮定が存在するので, それを無視して計算した平均値の差が因果効果を意味するとは限らない.
2.3 今回取り組む問題
動学構造推定はテクニカルでなんかすごいことをやってるという印象を簡単に与えられる. しかし, 今回は時間がないのでもう少し簡単にできるほうをやる. 前回話題にしたのは「動学的」構造推定であり, 時間変化を取り入れたモデルを扱うジャンルである. 一方で, 今回は考慮しない「静学的」構造推定の具体例を紹介する. といっても昔からある研究なので, すでに日本語の講義スライドもネット上に転がっていたりするし, もしかしたら発表者の中にも授業でやったことがあると言う人がいるかもしれない.
今回は特に, 生産関数の推定の問題を例にする. 生産関数をどういう形にするかはいろいろだが, よく使われるものの1つに コブ=ダグラス型生産関数がある9. 特に, 一企業の生産関数を,
\[\begin{aligned}Y=f(K,L):= & \alpha K^{\beta_{K}}L^{\beta_{L}}\end{aligned}\]
という指数関数で表す10. \(\alpha,\beta_{K},\beta_{L}\) はパラメータである. \(\beta_{K}=\beta_{L}=0.5\) の場合, 図2.1 のような形状になる.)
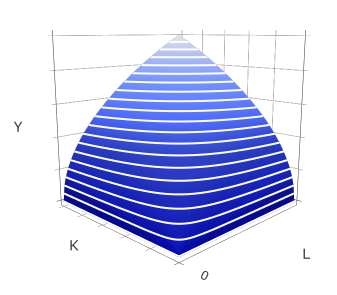
図2.1: コブ=ダグラス生産関数の形状
References
Lucas, Robert E. 1976. “Econometric Policy Evaluation: A Critique.” Carnegie-Rochester Confer. Series on Public Policy 1 (C): 19–46. https://doi.org/10.1016/S0167-2231(76)80003-6.
Lütkepohl, Helmut. 2007. New Introduction to Multiple Time Series Analysis. 1. ed., corr. 2. printing. Berlin: Springer.
Merton, Robert C. 1974. “On the Pricing of Corporate Debt: The Risk Structure of Interest Rates.” The Journal of Finance 29 (2): 449. https://doi.org/10.2307/2978814.
Reiss, Peter C., and Frank A. Wolak. 2007. “Structural Econometric Modeling: Rationales and Examples from Industrial Organization.” In Handbook of Econometrics, edited by James J. Heckman and Edward E. Leamer, 6:4277–4415. Handbook of Econometrics. Elsevier. https://doi.org/10.1016/S1573-4412(07)06064-3.
Scott, Steven L., and Hal R. Varian. 2014. “Predicting the Present with Bayesian Structural Time Series.” International Journal of Mathematical Modelling and Numerical Optimisation 5 (1/2): 4. https://doi.org/10.1504/IJMMNO.2014.059942.
簡単な定義と特徴は[https://qiita.com/saltcooky/items/2d0119ea4a10bab6cff2]の最後のほうに書いてある. より詳しい話を知りたければ, 沖本 (2010) が言及している. インターネットの日本語圏で出回っている情報の多くはこのあたりからだと思うが, もっと多変量時系列モデルを知りたいなら Lütkepohl (2007) の教科書がある (この本は約700ページの間, タイトル通りマジで多変量時系列モデルのことしか書いてない). 時系列モデルに関する本は 北川 (2005) の教科書を始め和書でも多く出ているが, 経済学や数理ファイナンスの観点から書いたもの以外では, 構造VARについて言及したものは私の知る範囲では見られない. 構造VARという考え方自体がパラメータの識別を前提としているからだろう. マクロ経済学における時系列モデルの利用を知りたいのなら, 渡部 (2016), 中島 and 渡部 (2012) が参考になる. 本格的な教科書は専門外なので知らない.↩
そのため, VARでも因果関係を定義できるということでGranger因果性が注目を集めた. つまり, 以前の投稿で問題にした, 予測か因果かという二択は, 経済学の発展のなかでもしばしば議論されてきた問題だということがわかる.↩
正確には少し違うが, 重要なのはサンプルの平均的な差を見るという特徴が共通している↩
構造推定に使うような, 経済現象の構造を表したモデルを, 平均の差の比較という因果推論のフレームワークで推定できるように単純な形に変形することからこう呼ばれる. この式変形のため, 根本的な構造パラメータを特定しづらいという問題がある.↩
歴史的経緯は 北村 (2016) などが少しだけ解説している. 計量経済学の観点では統計モデルとして Hayashi (2000), Ch. 8 で言及している. また, Cameron and Trivedi (2005), Ch. 2 は教科書の最序盤で構造モデルと誘導モデルの特徴付けを行うという独特の構成になっている.↩
そういえばこの用語で呼び始めたのは一体誰なのだろうか? たぶんRubinではない.↩
後者の因果推論フレームワークも, もともとは counterfactual causal modelと呼ばれていたが, (おそらくはこの性質の違いのため)少なくとも経済学の分野では最近はあまり強調されていない気がする.↩
他にも色々あるが, 例えば物理学のように法則がかなり明確になっている分野を勉強した人間からはおかしなことのように聞こえるかもしれない. しかし, 経済学ではむしろ, 変に特定化すれば特定化の誤りを免れない.↩
生産関数のより詳しい数学的性質はミクロ経済学の教科書に書かれている. 例えば, 特に有名なのは 西村 (1990), 『ミクロ経済分析』(Varian 1992), Mas-Colell, Whinston, and Green (1995) などである. それ以降にも評価の高いミクロ経済学の和書がいくつかでているが, 私はあまり読んでいないのでなんとも言えない.↩